WARPLab 7
- Downloads
Getting Started
- Sample Buffer Sizes
- Automatic Gain Control
- Examples
- Extending WARPLab
- Debugging Errors
- Porting Code
- Benchmarks
WARPLab 7 Framework
WARPLab 7 Reference Design
Reference Design Modules
- Node
Interface Group
Baseband
Transport
Trigger Manager
Hardware
WARPLab 7 Example: SISO OFDM
File: wl_example_siso_ofdm_txrx.m
This WARPLab example implements a simple OFDM transmitter and receiver. The script can run with WARP hardware in the loop or it can run as a standalone MATLAB simulation of a complete OFDM transmitter and receiver. The MATLAB code does not require any MATLAB toolboxes that are not provided in a basic installation.
Important: this script is not intended as a tutorial of OFDM. If you're not already familiar with the basics of OFDM please start with one of the many good OFDM tutorials available online. You will need to know the basics of OFDM before understanding the Tx and Rx processing in this example.
Transmitter

The OFDM transmitter code implements the following functions:
- Random data generation
- Modulation of random data to complex constellation symbols
- Mapping of symbols to data-bearing subcarriers
- Insertion of pilot tones in pilot subcarriers
- Inverse fast Fourier transform (IFFT)
- Cyclic prefix insertion
- Preamble construction and insertion
- Interpolation by 2x
Receiver
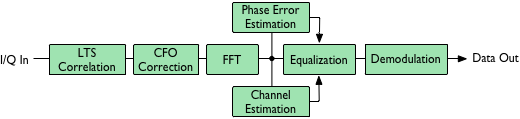
The OFDM receiver code implements the following functions:
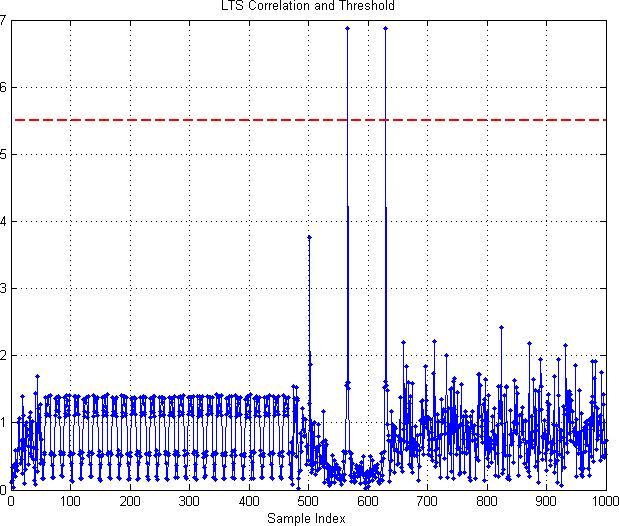
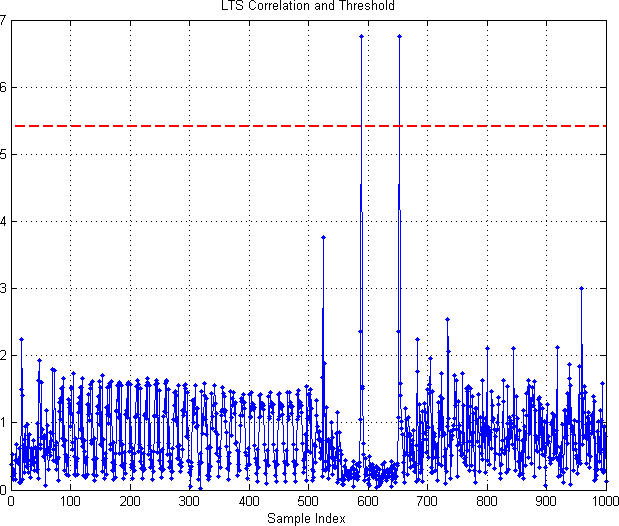
- LTS correlation for synchronization
- CFO estimation and correction use time-domain estimation from LTS
- Cyclic prefix removal
- Fast Fourier transform (FFT)
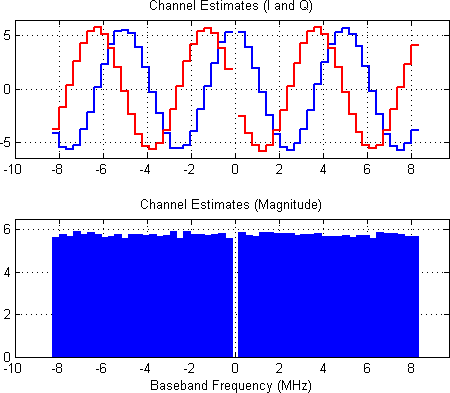
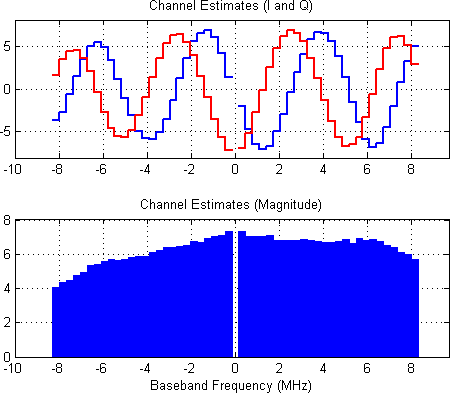
- Channel estimation from frequency-domain LTS
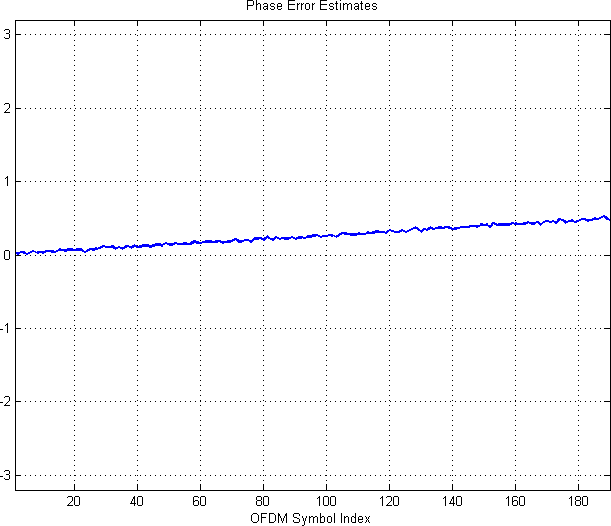
- Residual phase error estimation from frequency-domain pilot tones
- SFO estimation and correction from frequency-domain pilot tones
- Equalization of data-bearing subcarriers using channel estimates and phase error estimates
- Demodulation of complex symbols to data values
Running the Example
The WARPLab OFDM example can be used in simulation-only mode and in hardware-in-the-loop mode.
Simulation
To use the example in simulation mode set the top-level param USE_WARPLAB_TXRX = 0;, then run the m-script. When the script finishes 6 plots will show:
By default the simulation script applies AWGN with an arbitrary fixed SNR. You can change the simulated propagation characteristics in the m-code. Search for AWGN and apply whatever Tx->Rx degradations you like.
For example to simulate a perfect (noiseless) link, set the noise power to zero:
rx_vec_air = tx_vec_air + 0*complex(randn(1,length(tx_vec_air)), randn(1,length(tx_vec_air)));
The script also prints statistics about the experiment to the MATLAB command prompt:
Results: Num Bytes: 4560 Sym Errors: 0 (of 9120 total symbols) Bit Errors: 0 (of 36480 total bits) EVM: 3.779% LTS CFO Est: -0.07 kHz
Hardware in the Loop
Requirements: 2 WARP v3 kits, 1 antenna each.
To use the example with WARP hardware you will need two WARP nodes each running WARPLab 7.3 (or later) and a WARPLab environment setup on your PC. Refer to the WARPLab Quick Start if you have not yet setup WARPLab.
To target WARP hardware set the top-level param USE_WARPLAB_TXRX = 1;, then run the m-script. When the script finishes 6 plots will show:
The script also prints statistics about the experiment to the MATLAB command prompt:
Results: Num Bytes: 4560 Sym Errors: 0 (of 9120 total symbols) Bit Errors: 0 (of 36480 total bits) EVM: 4.541% LTS CFO Est: 2.64 kHz
CFO, Phase Error, and SFO
Typically, a transmitter and receiver are each clocked independently. This independence manifests in three different degradations that must be dealt with by a wireless receiver:
- Carrier Frequency Offset (CFO) - The center frequency of the transmitter will not perfectly match the center frequency of the receiver. Unless corrected, this will de-orthogonalize the OFDM subcarriers and cause inter-carrier interference (ICI). CFO is typically corrected in the time domain via multiplication with a digital carrier whose frequency negates the CFO estimate. This example uses a technique that compares two sequential preamble training symbols to estimate the CFO [1].
- Phase Error - Even after CFO is corrected in the time domain, there is typically a residual phase error component that must be corrected in the frequency domain and tracked over time. OFDM systems employ multiple pilot subcarriers to enable this correction system. All data subcarriers in each OFDM symbol are phase-rotated to match any residual rotation observed in the known pilots.
- Sampling Frequency Offset (SFO) - The temporal duration of a sample is slightly different at the receiver and transmitter due to different sampling clocks. Over the course of a reception, the relative sample periods will drift apart from one another. This manifests as larger phase error for the outer subcarriers [2]. Each data subcarrier in each OFDM symbol is phase-rotated differently according to its subcarrier index.
At the top of the script, there are three control variables that toggle three different correction systems: DO_APPLY_CFO_CORRECTION, DO_APPLY_PHASE_ERR_CORRECTION, DO_APPLY_SFO_CORRECTION. In this section, we will explore what happens when different combinations of these correction systems are enabled or disabled.
Scenario A
CFO Correction: Enabled Phase Error Correction: Enabled SFO Correction: Enabled
 1. Phase Error Estimates and SFO Correction Matrix | 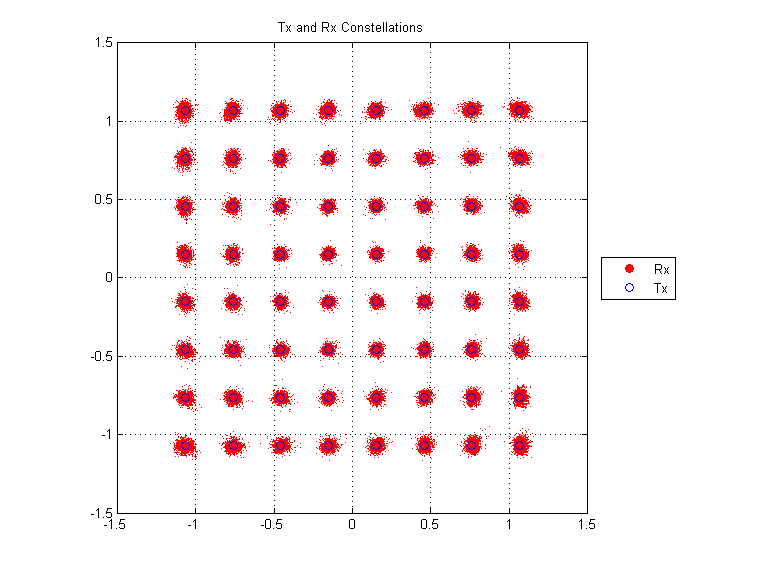 2. Rx Constellation | 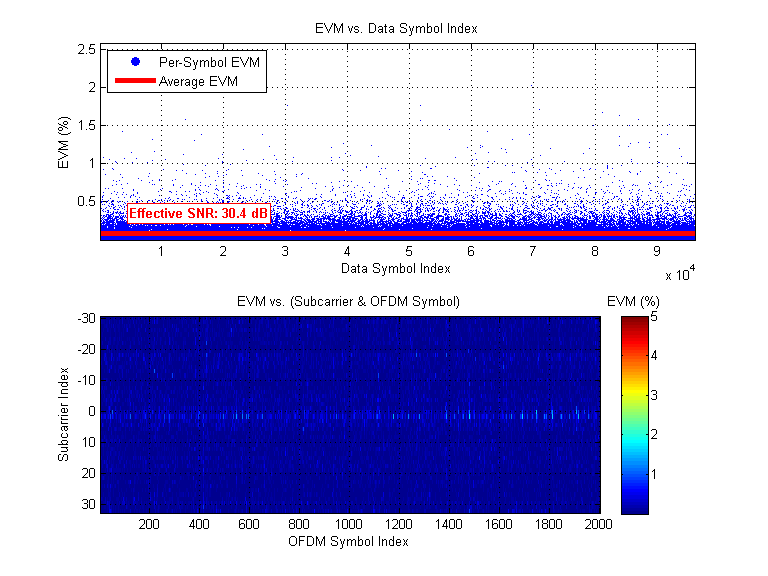 3. Error Vector Magnitude (EVM) and effective SNR |
The above plots are provided for reference. They show an example of how the receiver performs when all three correction systems are enabled.
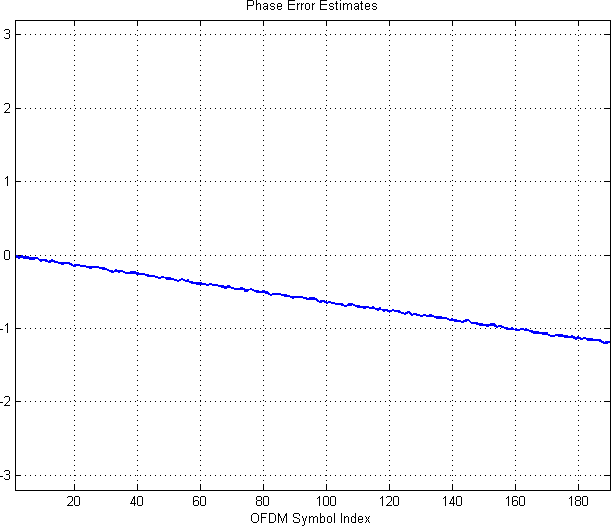
- The "Phase Error Estimates" plot shows a nominal phase twist for each OFDM symbol over the course of the reception. The "SFO Correction Matrix" shows a phase correction that increases for outer subcarriers over the course of the reception.
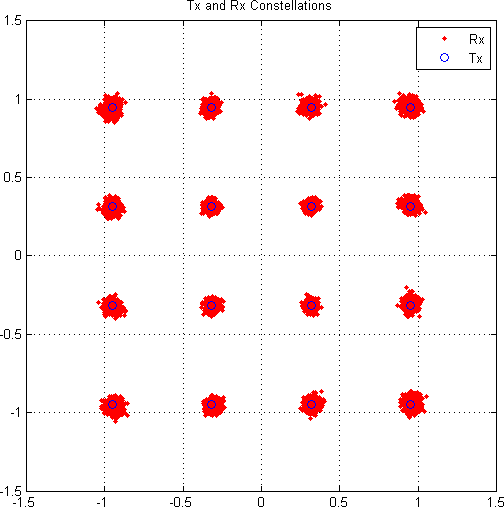
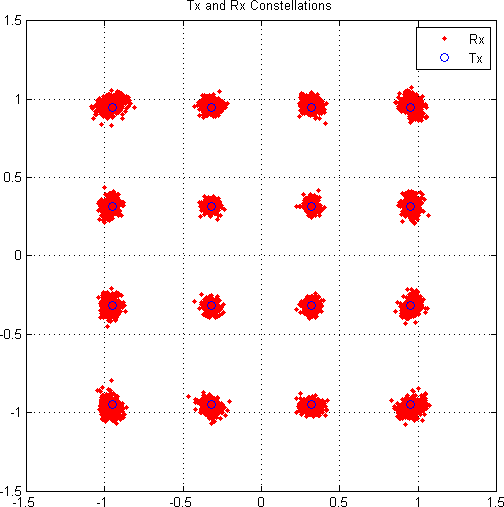
- The "Rx Constellation" plot shows each received symbol overlaid on each transmitted symbol.
- The "EVM and SNR" plot shows that EVM is small and has little dependence on OFDM symbol index or subcarrier index. Furthermore, the red line shows the effective SNR of the reception (calculated from the EVM values themselves).
Scenario B
CFO Correction: Disabled Phase Error Correction: Enabled SFO Correction: Enabled
 1. Phase Error Estimates and SFO Correction Matrix |  2. Rx Constellation | 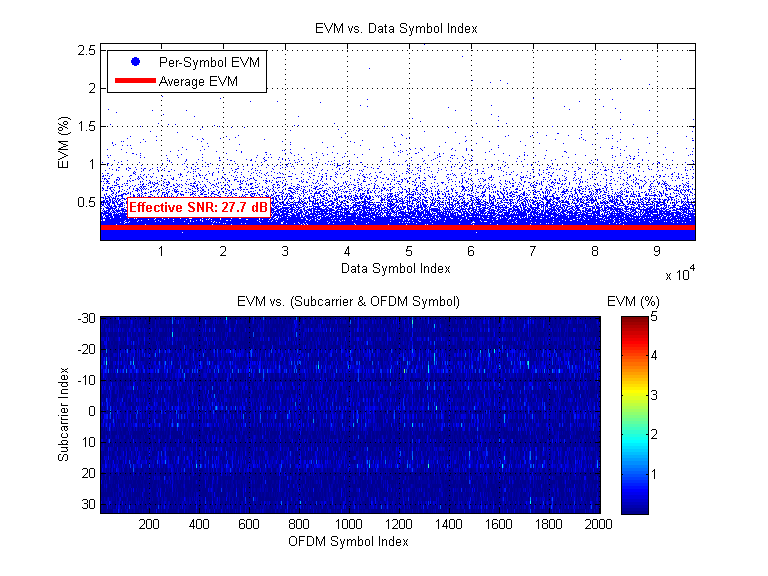 3. Error Vector Magnitude (EVM) and effective SNR |
By disabling time-domain CFO correction, we have increased the burden on the phase error correction system. In effect, the residual CFO to be corrected is now considerably larger. This can be observed by comparing "Phase Error Estimates" plot in this section with the equivalent plot presented in Scenario A. The number of 2π wraps is considerably larger than the previous scenario where time-domain CFO correction was enabled. Ultimately, however, phase error correction can only go so far. By the time the system is applying phase corrections in the frequency domain, ICI has already occurred because the transmitter's IFFT operation is not aligned to the receiver's FFT operation. This can be observed in the "EVM and SNR" plots where the effective SNR is a couple of dB worse than the previous case.
Scenario C
CFO Correction: Disabled Phase Error Correction: Disabled SFO Correction: Enabled
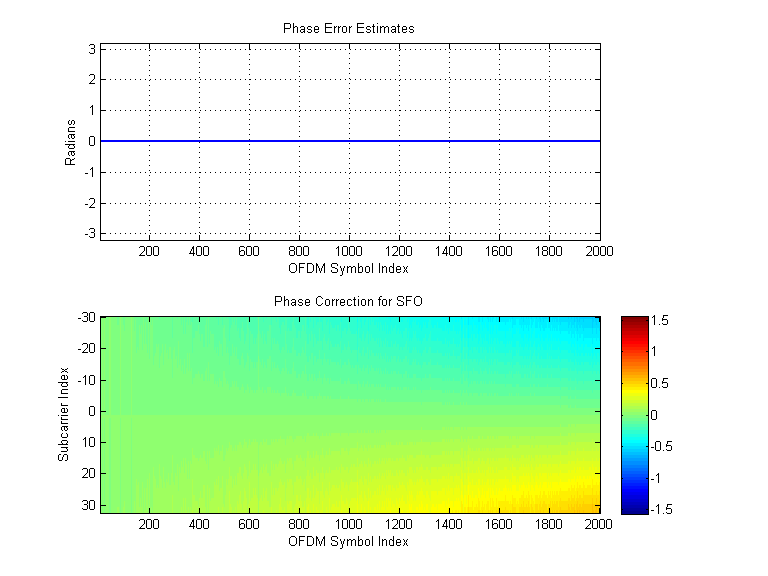 1. Phase Error Estimates and SFO Correction Matrix |  2. Rx Constellation | 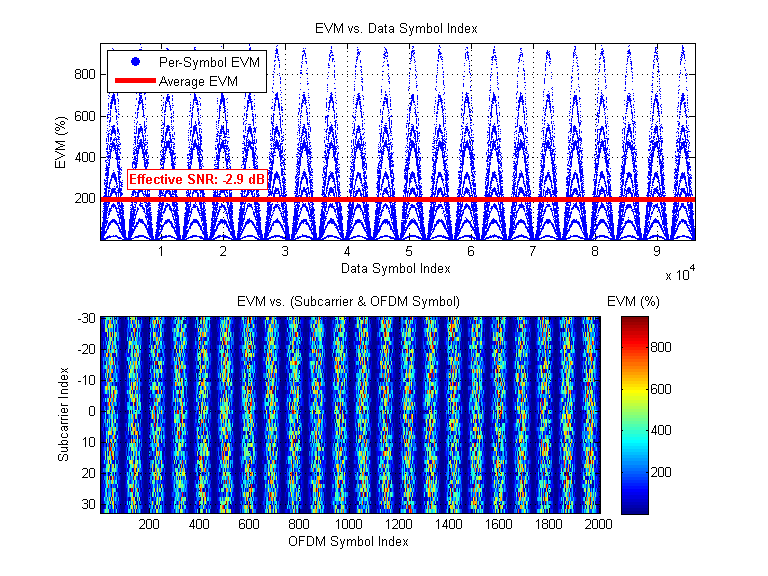 3. Error Vector Magnitude (EVM) and effective SNR |
When both CFO correction and Phase Error correction are disabled, there is nothing to counteract the differing center frequencies of the transmitter and receiver. The result is a received constellation that "spins" around the complex plane. The speed of this spin is CFO. The "beat patterns" of high and low EVM are caused by the receive constellation periodically aligning to the transmitted constellation as it rotates around the complex plane.
Scenario D
CFO Correction: Enabled Phase Error Correction: Enabled SFO Correction: Disabled
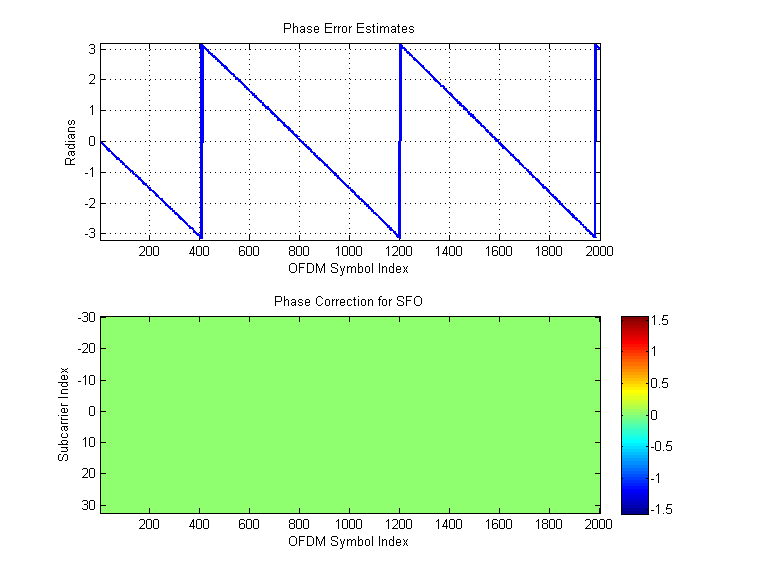 1. Phase Error Estimates and SFO Correction Matrix | 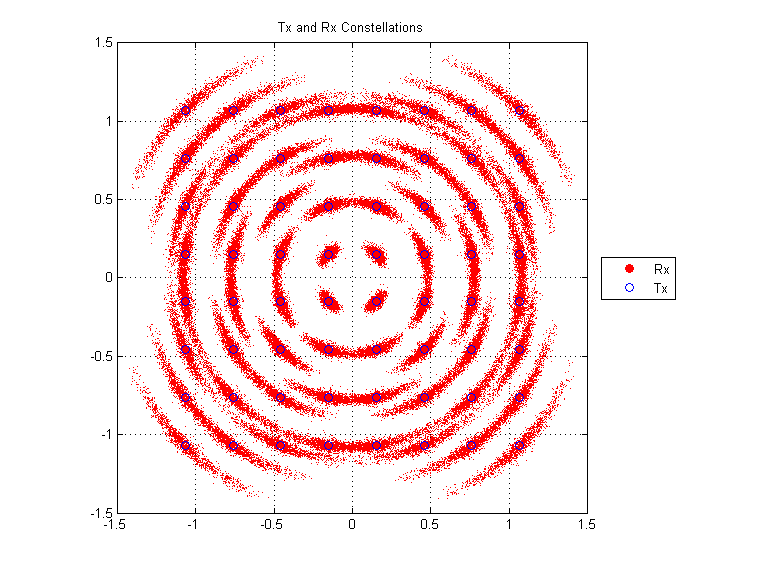 2. Rx Constellation | 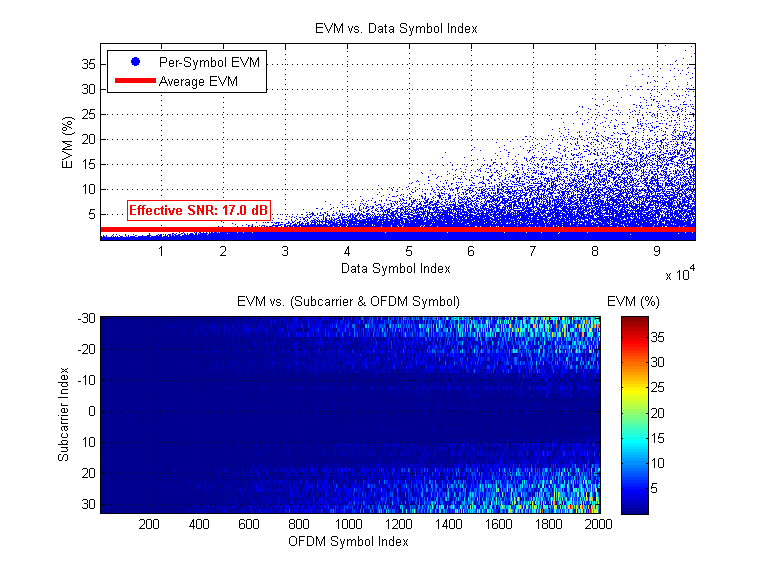 3. Error Vector Magnitude (EVM) and effective SNR |
Finally, we have re-enabled both time-domain CFO correction and Phase Error correction. We have disabled SFO correction. As the sample clocks drift over the duration of the reception, EVM begins to increase on the outer subcarriers.
Limitations
This example is intended as a starting point for researchers wishing to use WARPLab to prototype a wireless communications link. This examples does not implement some some blocks common in deployed OFDM systems, such as scrambling, interleaving and error correcting coding. For an example of a real-time OFDM implementation that implements all of these subsystems, please see the PHY in the 802.11 Reference Design.
References
[1] Schmidl, Timothy M., and Donald C. Cox. "Robust frequency and timing synchronization for OFDM." Communications, IEEE Transactions on 45.12 (1997): 1613-1621.
[2] Speth, Michael, et al. "Optimum receiver design for wireless broad-band systems using OFDM. I." Communications, IEEE Transactions on 47.11 (1999): 1668-1677.
Attachments (28)
- wl_ofdm_plots_hw_rxIQ.png (21.5 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_txIQ.png (21.1 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_chanEst.png (13.6 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_constellations.png (18.8 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_ltsCorr.png (27.6 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_phaseError.png (14.4 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_rxIQ.2.png (21.0 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_hw_txIQ.2.png (21.1 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_sim_chanEst.png (13.0 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_sim_constellations.png (17.0 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_sim_ltsCorr.png (25.9 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_sim_phaseError.png (14.7 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_sim_rxIQ.png (21.4 KB) - added by murphpo 10 years ago.
- wl_ofdm_plots_sim_txIQ.png (21.1 KB) - added by murphpo 10 years ago.
- wl_ofdm_blkDiag_Rx.png (15.6 KB) - added by murphpo 10 years ago.
- wl_ofdm_blkDiag_Tx.png (9.7 KB) - added by murphpo 10 years ago.
- Cy_PEy_Sy_phaseError.png (16.2 KB) - added by chunter 8 years ago.
- Cy_PEy_Sy_evm.png (33.3 KB) - added by chunter 8 years ago.
- Cy_PEy_Sy_constellations.png (18.2 KB) - added by chunter 8 years ago.
- Cy_PEy_Sn_phaseError.png (10.4 KB) - added by chunter 8 years ago.
- Cy_PEy_Sn_evm.png (40.3 KB) - added by chunter 8 years ago.
- Cy_PEy_Sn_constellations.png (39.2 KB) - added by chunter 8 years ago.
- Cn_PEy_Sy_phaseError.png (16.9 KB) - added by chunter 8 years ago.
- Cn_PEy_Sy_evm.png (42.8 KB) - added by chunter 8 years ago.
- Cn_PEy_Sy_constellations.png (21.7 KB) - added by chunter 8 years ago.
- Cn_PEn_Sy_phaseError.png (14.1 KB) - added by chunter 8 years ago.
- Cn_PEn_Sy_evm.png (64.8 KB) - added by chunter 8 years ago.
- Cn_PEn_Sy_constellations.png (53.0 KB) - added by chunter 8 years ago.
Download all attachments as: .zip